| 摘要:九年级数学期中期习题参考答案: 数学(01) 一、单项选择 1.B 2.C 3.D 4.C 5.A 6.B 7.D 8.B 二、 填空题 9. 12:5 1…… |
九年级数学期中期习题参考答案:
数学(01)
一、单项选择
1.B 2.C 3.D 4.C
5.A 6.B 7.D 8.B
二、填空题
9. 12:5
10. 18
11.
12.
13. 50
14.
三、解答题
15.
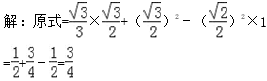
16.
17.
18. 解:如图
△A1B1C1就是所求的三角形,A1(﹣2,﹣2),B1(1,﹣1),C1(﹣1.5,0)
19. 解:连接A″A′,
∵当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分.
∴AD=10,
∵钟面显示3点45分时,A点距桌面的高度为16公分,
∴A′C=16,
∴AO=A″O=6,
则钟面显示3点50分时,
∠A″OA′=30°,
∴A′A″=3,
∴A点距桌面的高度为:16+3=19公分.
20. 解:如图,可知四边形DCBE是矩形.
21. (1)解:
22. 解:过点B作BD⊥AC于D.
23. 解:
24.
数学(02)
一、选择题
1.D 2.C 3.B 4.A 5.C
6.A 7.B 8.A 9.B 10.D
二、填空题
11.(﹣3,1)
12.﹣1或4
13. x1=﹣2,x2=3
14. 100°
15.
16.①、④
三、解答题
17.x=3或x=-5
18.解:根据题意得抛物线的对称轴为直线x=4,
而抛物线在x轴上截得的线段长为8,
所以抛物线与x轴的两交点坐标为(0,0),(8,0),
设抛物线解析式为y=ax(x﹣8),
19.解:根据题意得:

20.解:设初中组共有x个队参加比赛,依题意列方程
答:初中组共有10个队参加比赛.
21.证明:
22.解:
(1)∵△=[﹣(2m+1)]2﹣4m(m+1)=1>0,
∴不论m为何值,方程总有两个不相等的实数根.
(2)由于无论m为何值,方程恒有两个不等实根,故若要△ABC为等腰三角形,那么必有一个解为8;
设AB=x1=8,则有:
82﹣8(2m+1)+m(m+1)=0,即:m2﹣15m+56=0,
解得:m1=7,m2=8.
则当△ABC为等腰三角形时,m的值为7或8.
23.解:
(1)证明:连接OE,并过点O作OF⊥CD.
∵BC切⊙O于点E,
∴OE⊥BC,OE=OA,
又∵AC为正方形ABCD的对角线,
∴∠ACB=∠ACD,
∴OF=OE=OA,
即:CD是⊙O的切线.
24.解:(1)由题意得:y=(50+x﹣40)
=﹣10x2+110x+2100(0<x≤15且x为整数);
(2)由(1)中的y与x的解析式配方得:y=﹣10(x﹣5.5)2+2402.5.
∵a=﹣10<0,∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
(3)当y=2200时,﹣10x2+110x+2100=2200,解得:x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
25.解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),
穿越到手机上阅读
● 编辑 : 娜娜 / 小威 / 沈晓沫
● 发布 : 晓沫 审核 : 朤朤 / 陌语
● 热线 : 158-1078-1908
● 邮箱: 770772751#qq.com (#改为@)





